| | | | x | 2 | 5 | 7 | 3 | 6 |
| | | | | 4 | 8 | 2 | 7 |
| | | |
|
| | | | 1 | 8 | 0 | 1 | 5 | 2 |
| + | | | 5 | 1 | 4 | 7 | 2 | |
| 2 | 0 | 5 | 8 | 8 | 8 | | |
| 1 | 0 | 2 | 9 | 4 | 4 | | | |
|
| 1 | 2 | 4 | 2 | 2 | 7 | 6 | 7 | 2 |
|
Цю сторінку присвячено математичним таблицям.
Історична довідка. Коли будь-яке обчислення вимагало кількох секунд (хвилин, півгодини, ...) рутинної роботи на папері,
дуже важливо було "про всяк випадок" записувати всі, в тому числі і проміжні, результати, бо подивитись на папірець завжди
було швидше та простіше, ніж повторити всі обчислення знову. Щоби обчислити приклад, що його наведено зліва, треба, навіть знаючи таблицю множення, витратити хвилини три-чотири. А якщо треба виконати обчислення
із застосуванням якихось елементарних функцій (y = sin(x) / (sqrt(tg(x*x)))), то отримання результату "в стовпчик"
стає справді карколомною задачею. "Без нічого" порахувати будь-яку елементарну фукнцію можна лише розвиненням її у тяд Тейлора.
Логарифмічні лінійки давали точність 2, рідко 3 значущі цифри.

Для тих, хто не ладен множити в стовпчик... |
Для більшої точності значення функцій обчислювалися подвижниками
наперед та друкувалися у вигляді окремих книжок. Володимир Модестович Брадис присвятив роки своїм обчисленням, що вилилися у
1921 році у книжку "Чотиризначні математичні таблиці", що видавалася-перевидавалася, мабуть, чи не сотню разів. Автор свого часу користувався
у школі виданням 1965 року, що йому перйшло від матері Галини Гнатівни — вчительки математики. Це 22-ге українське видання —
переклад з 32-го російського.
Збільшення точності вимагає наявності більш розрядних таблиць, але п'ятизначні таблиці, що просто
повторюють ті самі функції, будуть вдесятеро більш об'ємними... Тому детальніші таблиці випускалися більш спеціалізованими.
Як відбувалося подеколи створення таких таблиць, можна прочитати, наприклад, у часописі
"Мир ПК", № 10, 2005 рік.
В інтернеті продаються як букіністична екзотика, наприклад, такі видання:
- Хренов Л. Восьмизначные таблицы тригонометрических функций. М.: Наука, 1967. 467 с.
- И. Потерс. Шестизначные таблицы тригонометрических функций, содержащие значения шести тригонометрических
функций через каждые десять секунд дуги квадранта, разделенного на 90 градусов, и значения котангенсов и косекансов через
каждую секунду от 0 град. 0' до 1 град. 20'. 293 с. 27 см. 5-е изд. М. Недра 1978.
У другій половині сімдесятих років раптом, як гриби після дощу, стали з'являтися видання на кшалт останнього.
У цей час обчислювальні машини уже були досить поширеним явищем, мови програмування були вже дисить високого рівня, принаймні, всі елементарні функції
у них вже було реалізовано. Тому написати програму, яка би в циклі друкувала таблицю значень функції з будь-якою дискретністю,
було, як кажуть, справою техніки. Тому справді серйозні інженери та науковці вже мали можливість все, що їм треба, обчислювати на комп'ютері.
А у видавництвах наукової літератури все ще вважали півтисячи сторінок цифр науковим подвигом. Ну і спритні програмісти цим користувались.
Ні, якщо без горделивих жартів, то був короткий період, коли на машині вже можна було все порахувати,
але більшості практиків ЕОМ ще були не відомі. У цей час виникнення таких книжок справді було корисним. Але вони застаріли
так само швидко, як зараз застаріває комп'ютерна література про роботу з черговими версіями різних програм та операційних систем.

Угорські таблиці. Теж старе видання (1960 р.?) |

Пам'ять на паперових носiях... |
У моїй колекції, крім рідного шкільного примірника таблиць Брадіса, є угорський варіант таких таблиць,
який належав дідові мого друга Бейли. Ця книжечка цікава тим, що у ній є рукописні сторінки.
Володар, втративши через якісь обставини один аркуш, знайшов, певно, у знайомих інший примірник та рукою переписав подвійний
аркуш цифр. Так це було важливо для тих, хто користувався таблицями.
Ще про дві книги таблиць. Волею долі до мене потрапили видання
- Пятизначные таблицы логарифмов. Под ред. проф. Жуковского А. М. М.: Военное издательство Министерства вооружённых сил Союза СССР, 1946. — 196 c.
У цій книжці є цікава примітка у вихідних відоомостях: "Отпечатано с матриц под наблюдением капитана Верзилина М. Н.".
Сторінки мають особливі береги зі змістом відповідних сторінок (див.), як у блокнотах з абетками.
У додатку наведено математичні формули. Цікаво, що ті формули, що ми їх зараз називаємо тригонометричними, там названо
"Гоніометрія". Наведено формули розв'язання трикутників на площині, та НА СФЕРІ. Крім того, наведено таблицю переведення
колишніх російських мір та ваг у метричну систему. Ну, звідки б я дізнався, що 1 відро горілки = 10 штофам = 100 чаркам = 12,299 літру?
Таким чином, стандартна чарка на той час - це 123 г. Або, що 1 золотник = 4,27 г. Російське прислів'я "Мал золотник, да дорог" — саме про нього
(див.).
Л. М. Милн-Томпсон, Л. Дж. Комри. Четырехзначные математические таблицы. М.: Физматгиз, 1961. — 246 с.
Ця книга цікава тим, що її передруковано з оригіналу, як зазначено, "фотомеханическим способом". Тому у таблиці
англійські позначення функцій (напр., log x, tan x, tan-1 x замість ln x, tg x, arctg x) та десяткова крапка
ПОСЕРЕДИНІ РЯДКА замість коми. Наприклад, замість 0,123 пишеться ·123
(див.).
Ще одна цікава деталь з передмови авторів: "Порядок імен авторів на титульному аркуші було визначено підкиданням монети
та є, таким чином, цілком випадковим". От би декому з моїх сучасників такої ретельності у питаннях наукової етики...
Під скло - кожному! |
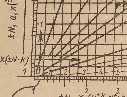
А тепер — про зовсім незвичний паперовий засіб лічби. Це — т. зв. "Універсальна обчислювальна номограма". У мене є в колекції книга
Патлах Д.И. Универсальная вычислительная номограмма: Метод быстрого счёта. — М.: Машиностроение, 1981. — 32 с.
Перше видання вийшло у 1953 році, а перші публікації Д.І.Патлаха на тему номографії відносяться до першої половини 30-х рр.

Якщо зламалася лінійка... |
До книги додається вкладка — аркуш 46 на 36 см. — власне, сама номограма. Її пропонувалося покласти на робочому столі під
скло, щоби вона завжди була під рукою. "В отдельных случаях номограмму целесообразно наклеить на картон". Фактично вона є сукупністю графіків степенево-показникових функцій. На одній шкалі, наприклад,
відкладається число N, на іншій — k, а десь на перетині якихось хитрих ліній читаємо значення Nk, або
N1/k, або logkN тощо. Приклад показано на фото. Показано обчислення
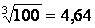 ,
але це можна трактувати і як ,
але це можна трактувати і як
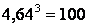 ,
або навіть ,
або навіть
 .
Точність результату — щонайбільше 2 розряди. .
Точність результату — щонайбільше 2 розряди.
|
