Мої улюблені задачки
|
| Надсилайте ваші відповіді на ці задачі милом - автор береться прорецензувати їх та відповісти |
Зустрілися двоє старих шкільних приятелів. Те та се, як справи, як сім'я. Аж один і каже:
- У мене троє дітей!
- А скільки ж їм уже років?
А цей зануда і каже:
- Добуток кількостей років моїх дітей дорівнює 36, а сума - оно номеру трамвая, що якраз повз нас проїздить.
Другий товариш (а вони колись вчилися на прикладній математиці) заходився розв'язувати задачу, але бачить, що дано дві умови на три невідомі величини, хоч і у цілих числах, та й каже:
- Ти як хочеш, а умов недостатньо.
- Автор дивиться і собі: справді - недовизначеність. Каже:
- А старший у мене - рудий!
- От так би і казав одразу! - відповідає йому приятель і дає правильну відповідь.
Питається в задачі: скільки ж років тим бісовим дітям?
Коли та чому кава буде гарячішою:
Дано: дві однакові кімнати - прямокутні паралелепіпеди, оздоблені зсередини однаковим однорідним матеріалом. У строгому центрі кожної кімати знаходиться правильна куля з якогось однорідного матеріалу, наприклад, з металу (скажімо, хром-никелева сталь 18/10).
Відміна полягає у тому, що одна куля висить на абсолютно тонкій нитці, що не розтягується, не проводить тепло та не є екраном, а друга стоїть на стрижні з такими самими властивостями.
У деякий момент всі стінки обох кімнат абсолютно рівномірно та однаково починають нагріватися за однаковим законом T(t) (температура від часу).
Яка куля буде нагріватися швидше і чому саме?
У мішку знаходиться куля, рівноймовірно біла або чорна. До неї долучають білу кулю такої самої форми. Потім, не глядячи, виймають одну з двох, і вона виявляється білою!
З якою ймовірністю куля, що залишилася у мішку, є білою?
Білу кулю знову кидають у торбинку, витягують кулю, яка виявляється білою.
З якою тепер ймовірністю куля, що залишилася у мішку, є білою?
Узагальніть результат на n спроб, якщо чорну кулю так і не вдається побачити.
Півтори курки за півтора дні несуть півтора яйця.
Скількі яєць одна курка несе за один день?
Попри елементарність розв'язання відповідь є досить несподіваною...
Дехто їде машиною з Ужгорода до Мукачева зі швидкістю 40 км/год. Біля с.Середнього (рівно посередині між цими містами) він раптом розуміє, що не встигає. З якою швидкістю треба їхати другу половину шляху, щоби середня швидкість за весь шлях була вдвічи більшою, тобто 80 км/год.?
Жив-був бідний художник один. І вирішив він купити букет квітів для коханої. І для цього він продав картини і дім.
Питається, за скільки пішла хатинка бідного художника, якщо він купив "міліон алих роз" по 10 грн. за штуку, а крім будинку, продав ще дві картини по 300 баксів кожна?
До чарівної принцеси женихаються N прекрасних принців. Сватів засилають послідовно. Принцеса, вислухавши пропозиції та оцінивши партію, може або погодитися та вийти заміж, або відмовити, і тоді гордий принц від'їжджає назавжди. Один раз відмовивши женихові, принцеса більше не може його повернути - гідність не дозволяє принцам повторювати пропозицію руки та серця вдруге.
Будемо ставити у відповідність кожному принцу деяку оцінку, що її дає йому принцеса, і будемо цю величину вважати випадковою з відомим розподілом (однаковим для всіх N достойників). Стратегія принцеси полягає у тому, щоби відмовивши певній кількості женихів, пристати на чергову пропозицію і тим визначити величину свого виграшу. В такому разі наступникам щасливця відмовлено a priori.
Як має діяти принцеса, щоби максимізувати свій виграш у ймовірнісному розумінні (тобто максимізувати матсподівання виграшу)? Кількість женихів N принцесі відома.
Ускладнений варіант задачі: функція розподілу функції якості принців є невідомою, але її та її параметри можна оцінити з виборки тих нещасних, кому вже відмовлено.
Варіант задачі, з умовами, геть наближеними до бойових: кількість женихів є невизначеною, але до принцеси надходить випадковий потік женихів, який локально можна вважати пуассонівським зі щільністю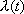 
, що зменшується, причому
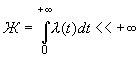
Я почав співробітничати з журналом "Пульс" профбюро студентів ННК "ІПСА" НТУУ "КПІ". У кожному числі маю намір публікувати по дві цікаві задачки. Після виходу чергових чисел журналу задачі будуть з'являтися і тут.
1. Тема: "Брехуни та правдиві".
На такому собі острові Труфолс живуть собі два племені — "брехунів" (вони на всі запитання відповідають виключно хибно) та "правдивих", тих, хто на всі запитання відповідають виключно правдиво.
Минулого року влітку я відпочивав на цьому острівці. Коли ми були приїхали, нас зустрічали двоє представників місцевої турфірми. Я звернувся до одного з них, бажаючи визначити, хто з них є хто, і відверто запитав: "Ви "брехун"?"
Він відповів: "Праложп к пфзукпр жфк пф". Другий, який знав українську, переклав: "Він сказав, що ні, але насправді — він таки брехун"...
Питацця у задачці: "Хто ж із них є хто"?
2. Тема "Запитайки". Один дурень може поставити стільки запитань, що і сто мудрих не зможуть відповісти.
Але Вам доведеться.
Так і не розібравшись зі звичаями населення дивного острова, ми попросили перевезти нас на сусідній — Такні, з доплатою.
На цьому острові жителі не переймаються тим, щоби взагалі відповідати на запитання прибульців. Вони самі запитують, і не відповісти тут означає кревну образу...
На острові Такні теж живуть два народи — "таки" та "ніки". "Таки" завжди ставлять запитання, на які треба відповідати "Так". "Ніки", відповідно, клінічно схиблені на тому, щоби запитати у Вас щось, на що Ви змушені будете відповісти "Ні".
Перше, що я почув від представника турфірми, що зустрічав мене в аеропорту, було: "Скажіть, пане, я — "нік""? Ну, і що я мав відповісти, а головне, хто ж цей чувак є?
1. Як розрізати куб, щоби площа перетину була максимальною7
2. Для того, щоби розпиляти дерев'яний куб 3х3х3 на 27 кубиків 1х1х1, достатньо шістьох розпилів.
Чи можна зменшити кількість розпилів, якщо після кожного розтину перекладати фрагменти, щоби за одне розпилювання розрізати не один, а більше фрагментів?