Реалізація дерева

РЕАЛІЗАЦІЯ ДЕРЕВА

Будуть розглядатися тільки двійкові дерева, хоча у принциповому плані можна запрограмувати і більш складні дерева.
У двійковому дереві кожна вершина i-го шару пов'язана з одною вершиною (i-1)-го шару - своїм предком - та з двома вершинами (i+1)-го шару - своїми потомками. При цьому потомки можуть бути фіктивними, тобто фактично не існувати.

Сфери застосування:

трансляція арифметичних виразів;
організація швидкого пошуку у великих масивах інформації;
організація зберігання та обробки спеціальної інформації;
генеалогічні дерева, дерева результатів спортивних змагань з кубковою системою, внутрішня структура деякої установи (управління, відділи) тощо.

Трансляція арифметичних виразів.

Існують три способи запису складних виразів. Для двомісних операцій (тут - Е) існують три способи запису:

префіксний (функціональний):

Е x y;

інфіксний (шкільний);

x Е y;

постфіксний (польский);

x y Е;

Всі три означають, що треба взяти операнди x та y (які можуть бути числами, тобто константами, змінними або іншими виразами) та виконати з ними операцію Е.

Приклад: вираз

(((A - B) * C) + (D / (E + F))) (1)

Звичайний (шкільний) спосіб - це інфіксний.

Для того, щоби організувати трансляцію такого виразу, слід розгорнути його у вигляді дерева. При цьому, що пізніше будуть виконуватися операції, то ближче до кореня дерева вони будуть розміщуватися у графі.

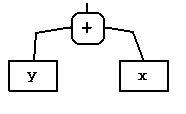
Наш вираз має структуру

x + y,

де x та y - деякі вирази. Тому його граф

Кожен з операторів має свою структуру:

x = ( ) * C;

y = D / ( ),

де вираз у дужках ще є виразом. Остаточно

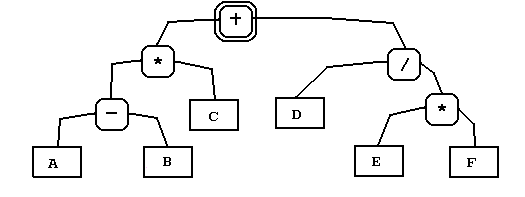
При трансляції, таким чином, першою операцією є побудова дерева.

Другою операцією є проходження його у деякому порядку. Порядок проходження може бути різним у залежності від мети обходження. Для транслятора зручніше за все реалізувати пост- або префіксну форму.

Для даного прикладу її префіксна та постфіксна форми мають вигляд:

префіксна:

+ * - ABC / D + EF

постфіксна:

AB - C * DEF + / +

Обидві форми однозначно визначають порядок обчислення та не вимагають дужок.
Префіксна структура дуже зручно реалізується за допомогою рекурсивних процедур.
Постфіксна структура краще за все реалізується за допомогою стеку.

Для програмної реалізації дерева та методів його обробки слід ввести типи змінних для цього об'єкту:


type 
  PTree = ^TTree;
  TTree = record
    Item : TItem;
    left, right : ref
  end;

var 
  t: TTree;

Тоді дерево може будуватися шляхом запису деяких даних у поле Item та запису у left та right посилань на наступні елементи. У залежності від характеру інформації конкретне наповнення структури TTree може модифікуватися.

Продовжуючи приклад з трансляцією формул, запишемо тип даних


type 
  TArythm = ('+', '-', '*'. '/');

  PExpression = ^TExpression;
  TExpression = record
    case symbolType : (signes, number) of
    signes: (phi : TArythm;
             left, right: PExpression);
    number : (x: Real)
  end;

Кожен арифметичний вираз (TExpression) розглядається, таким чином, як деякий знак операції phi: TArythm, який поєднує лівий та правий операнди, що є, у свою чергу виразами. У разі, якщо вираз є просто числом, поле symbolType має бути встановлене у значення number, тоді це число зберігатиметься у змінній x, а посилання на інші підвирази відсутні.

Для прикладу розглянемо формування дерева для виразу (1). Для простоти будемо вважати, що замість операндів A .. F у виразі стоять цифри (однозначні числа). Тоді, якщо цей вираз читатиметься з вхідного потоку, то символ може бути лише

цифрою 0..9;
дужкою (, );
знаком операції +, -, *, /.

Тоді, якщо ми поступово будемо читати вираз посимвольно, то наші дії мають бути такими:

якщо прочитано символ "(", то це означає, що буде новий вираз, який стоїть у дужках. Слід утворити нову структуру. Далі має слідувати вираз - лівий операнд цієї структури.
якщо прочитано цифру, то слід утворити структуру для її зберігання, та повернутися на попередній шар - до операції.
якщо прочитано знак операції, то його слід записати у корень поточного піддерева і перейти до правого операнду.
якщо прочитано праву дужку ")", то утворення поточного піддерева закінчено; слід повернутися на попередній шар.

Останню фразу слід розуміти так, що має існувати механізм що буде дозволяти у поточному дереві дізнаватися, хто є вершиною вищого рівня. Це можна зробити двома шляхами.

По-перше, можна у структурі TExpression завести поле AOwner: PExpression що зберігатиме посилання на попередній корень.

По-друге, можна утворити спеціальний стек, у якому зберігатиметься ланцюжок послідовності вершин, вздовж якого слід повертатися.

Перш, ніж перейти до безпосеренього програмування, зробимо ще одне спрощення. Будемо вважати що кожен вираз, крім просто цифр, береться у дужки. Тому, якщо слід зробити, наприклад, дії

A + B - C * D + E

то це слід зробити так:

(((A + B) - (C * D)) + E)

Аналогічні перетворення зроблено і у (1).

Примітка. Це дуже жорсткі обмеження. Але їх зняття відноситься до нюансів цієї області програмування трансляторів - лексичного аналізу, які зараз не розглядаються.

З урахуванням того, що було сказано, програму можемо записати у такому вигляді:


const Enter = chr(13);
...
procedure ReadTree (var Now : PExpression);
var 
  c: char;
  i: -1 .. Nmax;
  stak: array [-1 .. Nmax] of PExpression;
 
begin
  new(Now);
  stack[-1] := Now;
  i := 0;
  Now^.left := Nil;  {Якщо буде введено}
  Now^.right := Nil; {пусту послідовність}

  repeat
    c := ReadKey;
    case c of
      '(' : begin
        stak [i] := Now;
        inc (i);
        new(Now);
        stak [i]^.SymbolType := signes;
        stak [i]^.left := Now;
      end;
      '+', '-', '*', '/': begin
        Now^.phi := c;
        new(Now);
        stak [i]^.right := Now;
        inc(i);
      end;
      '0'..'9': begin
        Now^.SymbolType := number;
        Now^..x := ord(c) - ord(0);
        dec(i);
        Now := stak [i];
      end;
      ')' : begin
        dec (i)
        Now := stak [i];
      end;
      Enter : ; {Це ознака закінчення}
     else
        writeln ('Це помилка');
    end {case}
  Until c = Enter;

end; {Процедури}

Це була програма утворення дерева. Обчислення виразу може бути здійснене за допомогою рекурсивної програми-функції:


function Express (t: TExpression): Real;
begin with t do
  if SymbolType = number
    then Express := x
    else
      case phi of
       '+' : Express := Express (left^) + Express (right^);
       '-' : Express := Express (left^) - Express (right^);
       '*' : Express := Express (left^) * Express (right^);
       '/' : Express := Express (left^) / Express (right^);
    end
end;

На початок