Методи: включення | вибору | бульбашки

 

СОРТУВАННЯ МАСИВІВ

 
Будемо розглядати алгоритми сортування "на місці", тобто такі, які практично не потребують додаткової пам'яті, роблячи майже усі обміни всередині масиву.
При цьому усі методи сортування є сенс поділити на дві групи:


За принципом дії розрізнятимемо
  1. сортування за допомогою включення (by insertion);
  2. сортування за допомогою вибору (by selection);
  3. сортування за допомогою обмінів (by exchange).

Вважатимемо надалі, що у програмі визначено масив 

type Items = array [1..n] of Item;
 ...
var a : Items;
сортування відбувається за значеннями ключів a.key.

 

Вправи.

  1. Запропонуйте, не заглядуючи у книжки, свій метод сортування. Викладіть його у вигляді блок-схеми. Напишіть по ній програму мовою Паскаль.
    Візьміть для прикладу масив з 4 чисел та вручну відсортуйте його за Вашим алгоритмом.

Контрольні питання.

  1. Що таке функція впорядкування?
  2. Який алгоритм сортування називається сталим?
  3. Які типи методів сортування існують у залежності від типу пам'яті, що використовується?
  4. Що таке сортування на місці?
  5. Назвіть характерні особливості сортування масивів, файлів.
  6. Класифікуйте методи сортування масивів за принципом дії.
  7. Назвіть показники ефективності алгоритму сортування.

 

На початок | Методи: включення | вибору | бульбашки

 

Прості методи сортування.

Метод прямого включення.

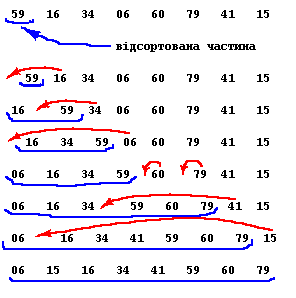
Один елемент завжди можна вважати відсортованим масивом довжини 1. Розглядаючи послідовно решту елементів масиву будемо включати їх у відсортовану частину масиву, ставлячи на потрібне місце, тобто не порушуючи відсортованості цієї частини. Повторивши операцію включення n-1 раз, одержимо відсортований масив.

Приклад. Візьмемо кілька випадкових чисел:

Example
Весь масив відсортовано.
На i-му кроці відсортованим вважається масив a[1] .. a[i], а вставляємо елемент a[i+1]. Вставляти можна, послідовно порівнюючи a[i+1] з a[1], a[2],..., поки не знайдеться "дірка" j
a[j] Ј a[i+1] Ј a[j+1].
Тоді слід зсунути елементи a[j+1] .. a[i] вправо на один елемент, а a[i+1] записати на місце a[j+1].
Може статися, що a[i+1] більше за будь-який з членів відсортованої частини. Тоді дірку не буде знайдено. Тому слід контролювати номер j, щоб не вийти за межи відсортованої частини.

Остаточно програма має вигляд 

procedure StraightInsertion (var a : Items);
var 
  i,j,k: integer; 
  x: Item;
begin
  for i :=2 to n do begin
    x := a[i]; j := 1;
    while x.key > a[j].key do inc(j);
    if j < i then {є дірка!} begin
      for k := i downto j+1 do
        a[k] := a[k-1];
      a[k-1] := x;
    end;
  end;
end

Аналіз. Кількість перевірок на i-му кроці дорівнює щонайбільше i-1, щонайменше 1, тому в середньому - i/2. Тому у середньому загальна кількість перевірок

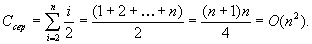
C_ave = (n+1)n/4
При цьому
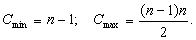
C_min=n-1; C_max = (n-1)n/2.
Кількість пересилань M дорівнює щонайбільше i, щонайменше 0 на i-му кроці, тобто i/2 у середньому. Тому
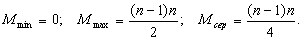
M_ave = (n-1)n/4
Той факт, що Mmin = 0, означає, що якщо масив з самого початку був відсортованим, то пересилань взагалі не відбувається, що свідчить про сталість методу. Поліпшення методу можливе за рахунок впровадження на першій стадії (пошук дірки) двійкового пошуку, бо частину масиву, де відбувається пошук, уже відсортовано.
Тоді на i-му кроці кількість перевірок становитиме log2, а загалом
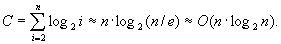
C = n log2(n/e) = O(n log2(n))

Кількість обмінів не змінюється, тому модифікація є незначною: обмін займає звичайно більше часу, особливо, якщо частина a[i].rest є значною.

Вправи.

  1. Модифікуйте програму StraightInsertion, впровадивши двійковий пошук замість рядка while...
  2. Згенеруйте масив на 100 та 10000 чисел за допомогою генератора випадкових чисел Random.
    Відсортуйте їх за допомогою обох програм, зафіксувавши час, що вони витратять на работу. Для звернення до машинового годинника витратіть функцію GetTime (Паскаль).

    3. Модифікуйте обидві програми, щоб вони рахували і виводили загальну кількість порівнянь та обмінів, тобто C та M.

Контрольні питання.

  1. Викладіть основну ідею методу простого включення.
  2. Наведіть характеристики якості методу простого включення (кількість порівнянь та обмінів).
  3. Як можна модифікувати метод простого включення ?

 

На початок | Методи: включення | вибору | бульбашки

 

Сортування за допомогою простого вибору.

  Основна ідея методу полягає в тому, що на кожному кроці шукається елемент, найменший з тих, що залишилися невпорядкованими, а після цього він додається до впорядкованої частини масиву останнім ( бо він там - найбільший).

a1 changes min
Якщо відшукано min, то він обмінюється значенням з першим елементом.

Потім операція повторюється для підмасиву a[2..n]:

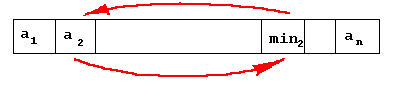
a2 changes min2
і. т. д..

Програма може мати вигляд: 

procedure StraightSelection;
var 
  i,j,k : Integer;
  r : Item;
begin
  for i := 1 to n-1 do {номер мінімуму} begin
    k := i; { шукати min серед a[i]..a[n] }
    for j := i+1 to n do
      if a[k] > a[j].key then begin
        k := j;
      end;
    {Тут a[k] - найменше з a[i]..a[n]}
    {Тепер обмін}
    if k <> i then begin
      r := a[k];
      a[k] := a[i];
      a[i] := r;
    end;
  end;
end;

Оцінимо якісні характеристики програми. На i-му кроці робиться (n-i) перевірок з елементами i+1, i+2, ..., n.
Тому

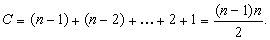
C = (n-1)n/2
Кількість обмінів у мінімальному випадку Mmin = 0, для забезпечення чого введено останній умовний оператор: якщо найменший елемент стоїть якраз на i-му місці, то перевіряти вже не слід. У найгіршому випадку кількість обмінів дорівнюватиме Mmax = n-1, бо на кожному кроці виконується тільки один обмін - поточного i-го елементу та відшуканого найменшого. Під час пошуку запам'ятовується ключ key, але це не може вважатися за обмін, бо повністю запис типу Item не переписується. Але навіть цю операцію можна видалити з програми, якщо замість ідентіфікатора min завжди писати a[k].key, а оператор
min := a[j].key
взагалі викинути з програми.

Принагідно зауважимо, що у [2,3], звідки взято ідею всіх методів, пропонується менш довершений варіант цього алгоритму з

Mmin № 0; Mmax = O(n2); Mсер = O(n ln(n))

На початок | Методи: включення | вибору | бульбашки

 

Сортування за допомогою простого обміну.

 

Це - найпростіший з методів сортування. Програма цього методу є найкоротшою з усіх можливих.
Ідея полягає у тому, щоб на кожному кроці, порівнюючи сусідні елементи між собою, міняти їх місцями, якщо вони стоять "не в тому порядку".
Таких проходів по масиву може знадобитися не менше, як (n-1), бо, якщо найменший елемент стоїть на останньому місці, то він досягне свого (першого) місця лише за n-1 крок сусідніх обмінів. 

Procedure BubbleSort;
var 
  i,j : Integer;
  x : Item;
begin
  for i := 1 to n-1 do
  for j := 2 to n do
    if a[j-1].key > a[j].key then begin {обмін}
      x := a[j];
      a[j] := a[j-1];
      a[j-1] := x;
  end;
end;

Програма називається "булькове сортування", а метод - методом "бульбашки", бо, якщо вважати кінець масива таким, що знаходиться угорі, то складається враження під час роботи програми, що елементи піднімаються по масиву, як бульбашки у воді до поверхні.
Ідея методу та його реалізація такі прості, що, скоріш за все, швидкісні характеристики його є найгіршими з усіх, що ми розглянули. Так воно і є.

Є багато способів поліпшити роботу алгоритму. Ми зробимо це, а потім проаналізуємо якість.
По-перше, після першого ж проходу ( при i = 1) найбільший елемент одразу підніметься на своє місце - останнє. Тому внутрішній цикл можна робити лише до (n - i + 1).
По-друге, якщо хоча б один елемент стоїть ще не на місці, то за черговий прохід буде зроблено принаймі один обмін. Тому, якщо за деякий прохід не зроблено жодного обміну, це означає, що масив уже відсортовано.
Тому слід перед кожним проходом встановлювати деяку логічну змінну y, рівну, скажімо, true, а в середині, якщо робиться обмін, то y := false. Після проходу її слід аналізувати.
Третю модіфікацію пов'язано з асиметриєю методу: якщо найбільший елемент потрапляє на місце лише за один прохід, то найменший - лише за n, якщо він стоїть на крайньому місці.
Тому пропонується проходи здійснювати по-черзі в двох напрямках. Такий спосіб називається шейкер-сортування (shaker (англ.)).

Кількість порівнянь для "булькового методу":

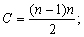
C = (n-1)n/2
обмінів:
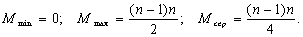
M_ave = (n-1)n/4

Для шейкер-методу аналіз зробити складно. Але цей метод має сильну перевагу якщо масив "майже відсортовано", тобто, коли кількість елементів m, що не стоять на місці, є незначною у порівнянні з n, n бб m. Тоді їх буде розставлено рівно за m проходів.

Вправи.

  1. Взявши за основу програму BubbleSort, здійсніть усі модифікації, про які тут говорено.
  2. Перевірте роботу програми відповідно до вправ 2 та 3 попередньої лекції.

Контрольні питання.

  1. У чому полягає основна ідея методу простого вибору?
  2. У чому полягає основна ідея методу простого обміну?
  3. Наведіть дані про кількість порівнянь та обмінів для методів простого вибору та простого обміну.
  4. Що таке метод "бульбашки"?
  5. Які існують модифікації методу простого обміну?
  6. Викладіть основну ідею шейкер-методу сортування?
  7. У яких випадках шейкер-метод має перевагу над методом "бульбашки"?

На початок | Методи: включення | вибору | бульбашки