РЕКУРСИВНІ ФУНКЦІЇ ТА АЛГОРИТМИ

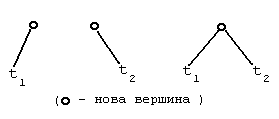
Взагалі багато об'єктів різної природи, не тільки функції, визначаються як рекурсивні.

Приклад 1. Множина натуральних чисел.

1. 1 - натуральне число;
2. Якщо n - натуральне число, то n+1 - натуральне число.

Приклад 2. Двійкові дерева.

1. o - дерево (пусте, одна изольована вершина).
2. якщо t1 та t2 - дерева, то є деревами.

Приклад 3.

ліва крива Дракона left(S1,S2) порядку 1	права крива Дракона right(S1,S2) порядку 1

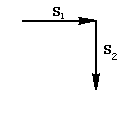
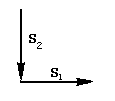
2) Якщо ( S₁, S₂, ..., S_2^n-1 ) - крива Дракона порядку n-1, то

- крива Дракона порядку n.

У програмуванні рекурсивними можуть бути не тільки функції, але й процедури (з цим ми познайомимося нижче).

При програмуванні рекурсії слід впевнитися у тому, що задачу не можна легше розв'язати за допомогою ітеративних процедур. Рекурсію використовувати варто тоді, коли нерекурсивний підхід сильно ускладнює програмування або не призводить до сильного зменшення часу роботи алгоритму, об'єму пам'яті для роботи тощо.

Приклади. Усі найбільш відомі приклади застосування рекурсії, фактично є прикладом того, як не слід застосовувати рекурсію.

1. n! := ( if n = 0 then 1 else n * (n-1)! );

Програмування цього фрагменту призведе до копіювання у сегмент стеку n рядків сегменту даних процедури обчислення факторіалу та адрес повернення.
Простіше написати

f := 1;
if n > 0 then
for i := 1 to n do
  f := f*i;

Ще більш контрастним є наступний приклад.

2. Біноміальні коефіцієнти:

    C(n,m) := (if (m = 0) or (m = n) 
                 then 1
                 else C(n-1,m-1) + C(n-1,m));

Це приведе до ~ 2ⁿ викликів процедурою C(n,m) самою себе з меншими параметрами. Між тим, багато викликів будуть дублюватися, буде багато викликів з однаковими параметрами. Навіть застосовуючи саме формулу біноміальної теореми, можна обмежитися лише (m + 1)(n - m + 1) викликів, що значно менше 2ⁿ при великих n. Але значно краще використати формулу

( 1 )

яка програмується за допомогою одного циклу і не призводить до переповнень розрядної сітки.

3. Числа Фібоначчі.

function Fibonacci (n: Word): LongInt;
begin
  if (n = 0) or (n = 1) then Fibonacci := n;
  else
    Fibonacci := Fibonacci(n-2) + Fibonacci(n-1)
end;

Попри свою "естетичну витонченість" вимагає 2ⁿ викликів, що може привести до переповнення стеку.

Але значно простіше числа Фібоначчі обчислити послідовно:

if (n = 0) or (n = 1)
  then f := n
  else begin
    f1 := 0; f2 := 1;
    for i = 1 to n begin
      f0 := f1;
      f1 := f2;
      f2 := f1 + f0;
    end;
  end;

Поступово зсуваючи значення, обчислюємо числа цього ряду, займаючи лише три комірки пам'яті та не дублюючи викликів з однаковими аргументами.

Не слід використовувати рекурсію, якщо є очевидний ітеративний розв'язок.

Будь-яку рекурсивну-перекурсивну програму врешті-решт ЕОМ перекладає у машинові коди, серед яких рекурсією і не пахне. Це означає, що будь-яку задачу можна розв'язати без застосування рекурсії. Але є випадки, коли застосування рекурсивних алгоритмів є виправданим. Це в першу чергу, область штучного інтелекту.

Приклади, що ми розглянемо далі, розглянуто у Н.Вірта [2,3] та у книзі [4], де всі програми викладено на Фортрані - мовою, що не дозволяє рекурсії.

Вправи.

1. Напишіть програму для обчислення біноміальних коефіцієнтів
   • через використання програми-функції для обчислення факторіалу;
   • без її використання - за допомогою формули (1).
   Визначіть область значень аргументів, для яких вона ще працює.
2. Напишіть програму-функцію, що для даного дійсного аргументу перевіряла б, чи є він натуральним числом. При цьому обов'язково використайте рекурсивне визначення натурального числа.

Контрольні питання.

1. Що таке рекурсія?
2. Що таке ітерація?
3. Чи існують задачі, що неможливо запрограмувати без застосування рекурсії? Наведіть приклади.

РЕКУРСИВНА ПРОГРАМА ПОШУКУ МІНІМУМА

Ясно, що якщо деякий масив поділити на дві частини, відшукати мінімальні елементи у обох частинах, а з них взяти менший, то це і буде мінімальний елемент у масиві. Якщо масив (підмасив) складається з одного елементу, то він і є найменшим.

Найменший елемент підмасиву a[n]..a[m] можна визначити як

Min(a, n, m) = min(Min(a, n, (n+m) / 2), Min(a, (n+m) / 2, m)), якщо n<m;
Min(a, n, m) = a[n], якщо n = m.

Тут через min(x, y) позначено менше з x та y, а через Min(a, n, m) - найменший елемент підмасиву a[n .. m].

Відповідна програма на Паскалі має вигляд

type arr = array[0..N-1] of Integer;
var a : arr;
 ...
function Min(var a: arr; n, m: 0..N-1): Integer;
var
  x,y : Integer;
begin 
  if n > m then Halt;
  if n = m then Min := a[n]
           else begin
             x := Min(a, n, (n+m) div 2]);
             y := Min(a, (n+m) div 2 + 1, m);
             if x < y then Min := x
                      else Min := y
           end
end;

На початок