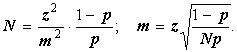|
Обчислення визначеного інтегралу методом Монте-Карло
| |||||
|
Лабораторні роботи |
В Архімеда була купель, до якої він примудрився зануритися сам, та власне, корона, яку він теж занурив у воду. У нас з вами є лише математична модель тієї корони у вигляді системи нерівностей, що дозволяють для будь-якої точки у декартовому просторі визначити її належність короні та виразити об'єм корони у вигляді кратного інтегралу. А ще є комп'ютер! Тому будемо застосовувати метод Монте-Карло. Мета роботи: навчитися одержувати оцінку визначеного інтегралу в умовах, коли аналітичне або чисельне інтегрування неможливе через будь-які причини. Початок | Теорія | Постановка задачі | Алгоритм | Планування експерименту
Визначення. Послідовність випадкових величин {xn} збігається за ймовірністю до випадкової величини x, якщо Закон великих чисел для схеми випробувань Бернуллі. Нехай проводиться N незалежних дослідів, у кожному з яких подія A або відбувається з ймовірністю p, або ні - з ймовірністю q = 1-p. Нехай серед N дослідів подія А відбулася у N* випадках, тоді
тобто, що більше ми будемо проводити дослідів, то точніше відношення N*/N буде давати оцінку справжнього значення ймовірності p, яке, можливо, є невідомим. Інтегральна теорема Муавра-Лапласа. Нехай x - біноміально розподілена випадкова величина з параметрами N (кількість випробувань) та p (ймовірність успіху). Тоді для -Ґ Ј a < b Ј +Ґ
тобто для досить великих N біноміальну випадкову величину можна вважати розподіленою нормально та використовувати для обчислення ймовірностей відповідні таблиці. Початок | Теорія | Постановка задачі | Алгоритм | Планування експерименту
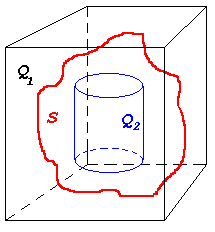
Початок | Теорія | Постановка задачі | Алгоритм | Планування експерименту Розв'язання. Опишімо навколо тіла, що досліджується, прямокутний паралелепіпед Q1, об'єм якого легко знайти, як добуток його габаритних розмірів. Нехай цей об'єм дорівнює V(Q1) = V1. Очевидно, що V Ј V1.
Якщо зробити достатню (N) кількість дослідів, то, порахувавши кількість точок, що "вцілили" у S, можемо оцінити
бо фундаментальною властивістю рівномірного розподілу є той факт, що ймовірність потрапити у довільну область пропорційна об'єму області та не залежить від її форми. Тоді приблизно
Початок | Теорія | Постановка задачі | Алгоритм | Планування експерименту Планування експерименту.
N* О B(N; p); M(N*) = Np; D(N*) = Npq; за теоремою Муавра-Лапласа випадкову величину
розподілено асимптотично нормально, h ® N(0;1). З іншої сторони,
де Далі за таблицею Ф(z) знаходимо для заданого a таке z, щоб Ф(z) = a. Тоді
звідки
Справжнє значення p невідоме, але зважаючи на вигляд графіку функції N(p), p О [0; 1] (суттєво спадна функція), зрозуміло, що, якщо оцінити p знизу, то одержимо оцінку N з перевишкою, що вдовольнить вимогам точності. Для оцінки p знизу впишемо у досліджуване тіло S інше тіло Q2 гарантовано меншого об'єму, який відносно легко обчислити. Позначимо
|
Mail-to: oselin@mmsa.ntu-kpi.kiev.ua
http://mmsa.ntu-kpi.kiev.ua/~oselin (KPI Intranet)
http://www.iasa.kiev.ua/~oselin
Copyright © Olexander Selin 2006 (web-design); Olexander Selin 2006 (content).
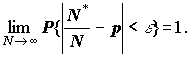
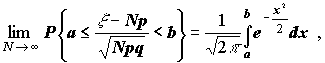
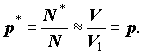
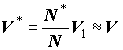
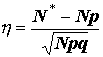
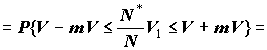
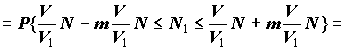
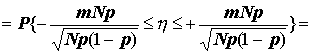
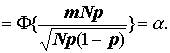
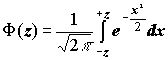 - функція Лапласа.
- функція Лапласа.