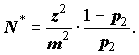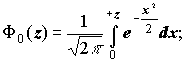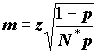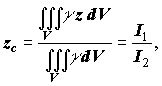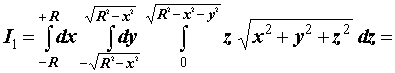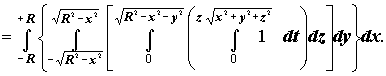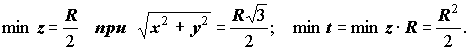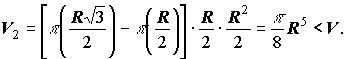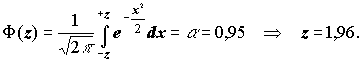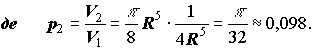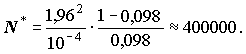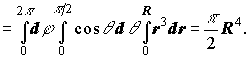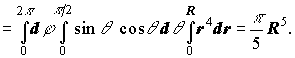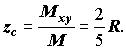Обчислення визначеного інтегралу методом Монте-Карло

— Це ж проблема Бен Бецалеля. Каліостро ж довів, що вона не має розв'язку.
— Ми самі знаємо, що вона не має розв'язку, — сказав Хунта, миттєво наїжачуючись. — Ми хочемо знати, як її розв'язувати.

Б. та Н. Стругацькі. Понеділок починається в суботу.

Лабораторні роботи

Початок | Хід роботи | Вимоги до звіту | Додаток

Як варіант Вам надано деякий кратний інтеграл, який треба обчислити, або задачу, що зводиться до обчислення кратного інтегралу.

Хід роботи:

Представити інтеграл у вигляді кратного інтегралу від функції f є 1 (у, можливо, багатовимірному просторі).
Описати навколо тіла, що утворилося, прямокутний паралелепіпед Q₁ більшого об'єму з гранями, паралельними координатним площинам.
Вписати всередину тіла S інше (Q₂) меншого об'єму V₂.
Написати програму, яка б генерувала випадкові точки, що гарантовано потрапляють у Q₁, а у S - з ймовірністю p.
Кількість точок оцінити за формулою
де m - припустиму відносну помилку оцінювання об'єму - узяти рівною 0,01; z - розв'язок рівняння
2Ф_o(z) = a.
a - надійна ймовірність, a = 0,95.
Відповідь сформулювати у формі надійного інтервалу: "З ймовірністю, не меншою за ... , можна стверджувати, що об'єм належить інтервалу [...; ...]". При цьому для обчислення довжини інтервалу треба виразити m з формули для N^*, підставивши у неї щойно обчислене p замість p₂:

Це буде оцінка реальної довжини надійного інтервала, який одержано для обчислюваного интеграла. Вона буде меншою за m = 0,01, від якого ми починали.
Оскільки індивідуальні варіанти - це приклади з задачників з математичного аналізу, то слід обчислити інтеграл аналітично та порівняти результати.

Початок | Хід роботи | Вимоги до звіту | Додаток

Звіт має містити:

умову задачі;
креслення;
аналітичний розв'язок;
обчислення оцінки N^*;
роздрук тексту програми, яку Ви написали;
роздрук результатів її роботи;
висновки та аналіз результатів.

Початок | Хід роботи | Вимоги до звіту | Додаток

Додаток

Приклад виконання попередньої роботи для ЛР№3

Задача: Знайти координати центру тяжіння півкулі

x² + y² + z² Ј R; z і 0,
якщо густина у кожній точці пропорційна відстані точки до центру кулі.
Розв'язання. Очевидно, що x_с = y_с = 0, тому будемо шукати z_с.

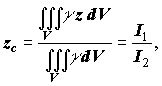
де густина

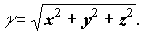
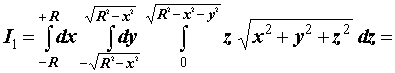
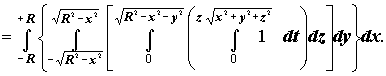
Паралелепіпед Q₁ = { (x,y,z,t) О R⁴ : x О [-R;+R]; y О [-R;+R]; z О [0;+R]; t О [0;+R ] } Н R⁴ , бо

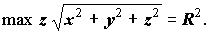
V₁ = 2R 2R R R² = 4R⁵ > V. Для оцінки V - объєму бодай-якого вписаного чотиривимірного тіла скористаємося такими міркуваннями:
якщо взяти кільце

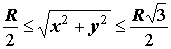
на площині XOY, то на цьому кільці

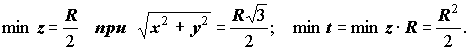
тоді чотиривимірне вписане тіло об'єму V₂ - з основою - кільцем та висотою по z = R/2 та по t = R²/2.

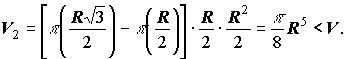
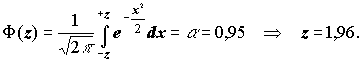
Бiльш точно z = 1,959963989.

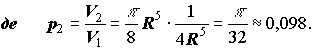
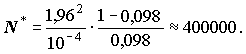
Алгоритм моделювання можна описати так.

N_S := 0; N_S - кількість точок у R⁴ , що потрапить у тіло S.
Цикл по i від 1 до N^*.
- Скориставшись функцією Random, згенерувати випадкову точку (x,y,z,t), координати якої розподілено рівномірно у діапазонах: -R Ј x Ј +R; -R Ј y Ј +R; 0 Ј z Ј +R; 0 Ј t Ј +R².
- Визначити, чи точка належить S. Це еквівалентне перевірці умов 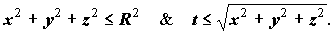Якщо так, то N_S := N_S + 1, якщо ні, то - ні.
Кінець циклу
Оцінка: V^* := N_S V₁ / N^*.

Значення N^* перевищує N, оцінкою зверху якого воно є. Тому треба переобчислити довжину надійного інтервалу m.
m := z Ц((1-p)/(N^*p), де p = V^*/V₁. Тлумачення результату: істинне значення інтегралу I₁ лежить у діапазоні [(1-m)V^*; (1+m)V^*] з ймовірністю 0,95.

Обчислення I₂ - маси тіла. Проводиться абсолютно аналогічно, лише у паралелепіпеді t О [0; R]; V₁ = 4R⁴; під час оцінювання V₂ min t = R. V₂ = pR⁴ / 8. Всі інші зміни є очевидними, обчислення проводяться аналогічно.
Остаточно:

z^* = I₁ / I₂.
Чи можна стверджувати, що z_c О [(1-m)z^*; (1+m)z^* ] з ймовірністю a = 0,95 ?

Аналітичне розв'язання.

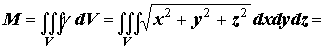
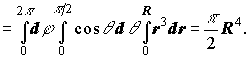
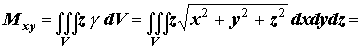
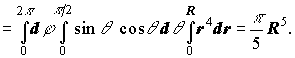
Тоді

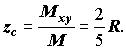
(Приклад 4, стор. 30, Н.В.Ефимов, Б.П.Демидович. Сборник задач...). До початку файлу

Повернутися до ЛР 3